Adott ABC háromszög csúcsaiból köröket szerkesztünk, majd az egyes körívek és a háromszög metszéspontjaira szakaszokat illesztünk. A szakaszokat felezőpontjuk körül 90 fokkal elforgatjuk, majd meghosszabbítjuk, ezzel megszerkesztve a háromszög belső szögfelezőit.
Tudjuk, hogy a szögfelező félegyenes azoknak a pontoknak a halmaza, amelyek egyenlő távolságra vannak a szög száraitól. Tekintsük a mellékelt ABC háromszöget ahol meghúztuk az A csúcsból induló fa és a B csúcsból induló fb belső szögfelezőt. Az fa szögfelező minden pontja egyenlő távol van a háromszög AC és AB oldalaitól. Az fb szögfelező minden pontja egyenlő távol van a háromszög AB és BC oldalaitól. A két szögfelező metszi egymást egy M pontban
Mivel M pont rajta van az fa szögfelezőn, ezért egyenlő távol van AB és AC oldalaktól, de rajta van fb szögfelezőn is, tehát egyenlő távol van AB és BC oldalaktól is. Ez azt jelenti, hogy az M pont egyenlő távol van a háromszög mindhárom oldalától, ezért az M pontnak illeszkednie kell a C csúcsból induló fc szögfelezőre.
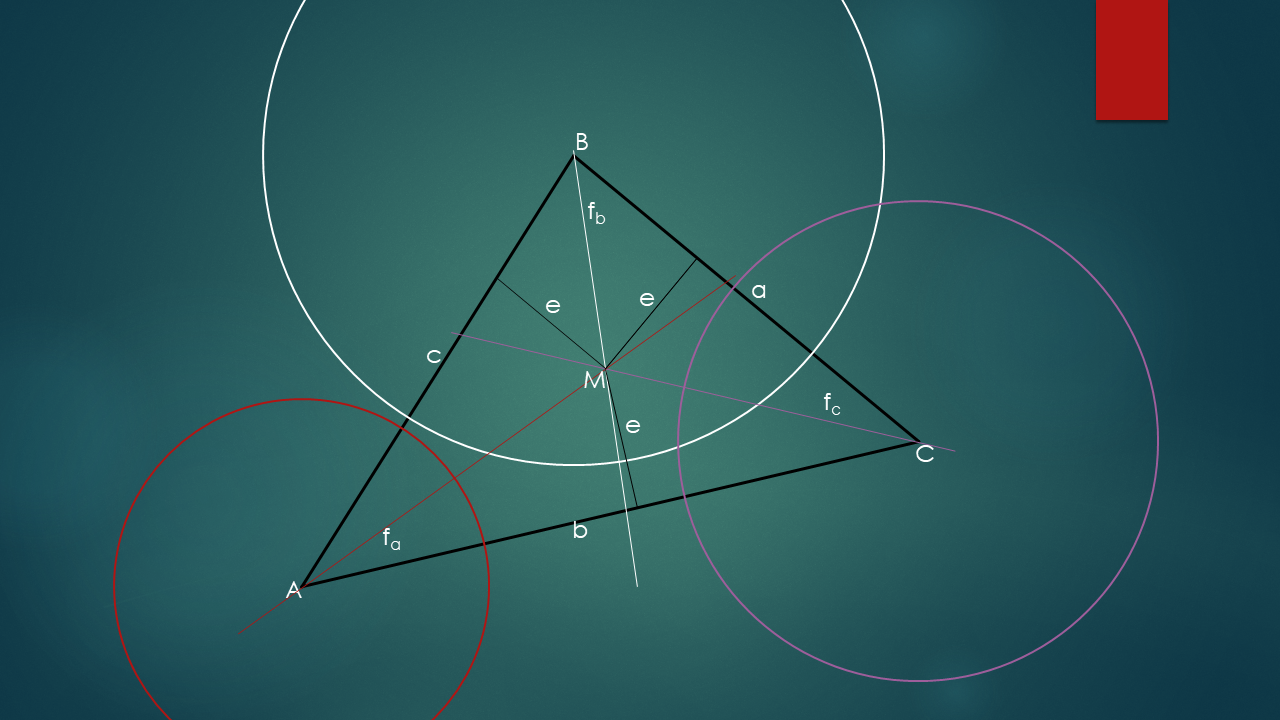
Ezzel bebizonyítottuk, hogy a háromszög szögfelezői egy pontban metszik egymást.
Bemutató videó: