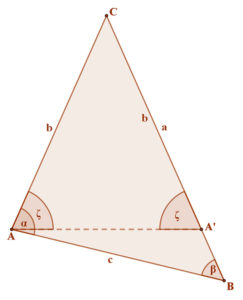
Legyen adott egy háromszög, amelyben AC < CB.
Azt kell belátnunk, hogy a nagyobb CB oldallal szemközti α szög nagyobb a kisebb AC oldallal szemközti β szögnél, azaz bizonyítandó, hogy ha AC < CB, akkor β < α.
Mérjük rá a rövidebb AC oldalt a hosszabbik CB oldalra a C csúcsból.
Így kapjuk az A’ pontot a CB szakasz belső pontjaként, illetve az AA’C egyenlőszárú háromszöget.
A fenti segédtétel alapján mondhatjuk, hogy A’AC∠=AA’C∠=ζ.
A α>ζ, hiszen AA’ egyenes az ABCΔ belsejében halad Másrészt ζ>β, mert ζ az AA’BΔ külső szöge.
Azt kaptuk tehát, hogy α>ζ >β, tehát α>β.