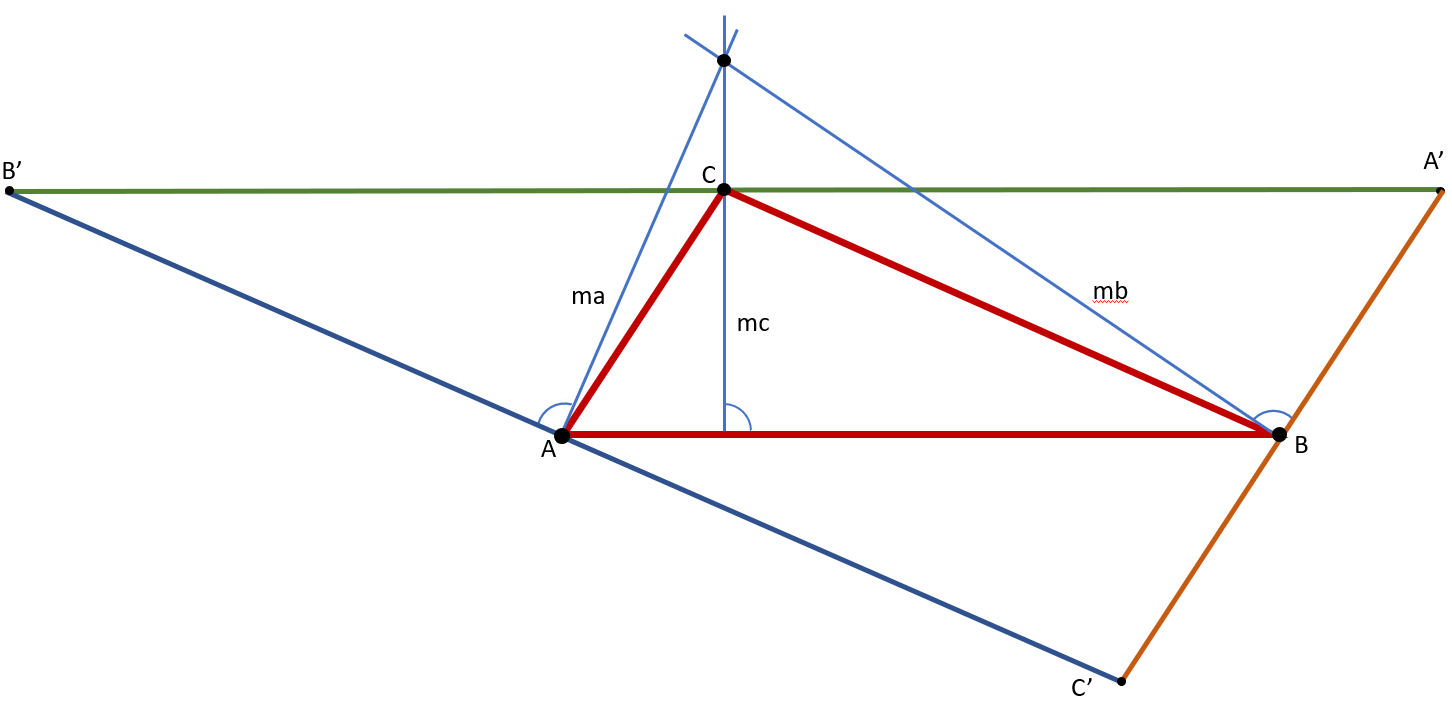
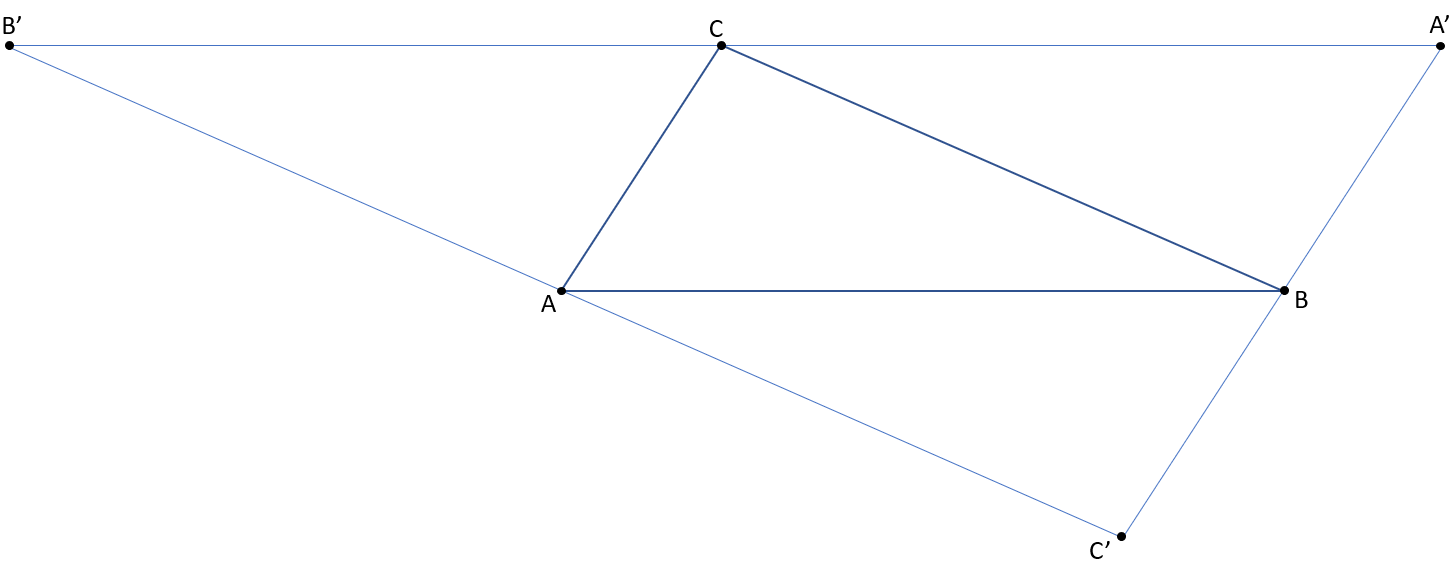
Vegyünk fel egy ABC háromszöget, majd annak a csúcsain át húzzunk párhuzamosokat a szemben levő oldalakkal. Az így keletkező háromszög csúcsai lesznek A', B' és C'
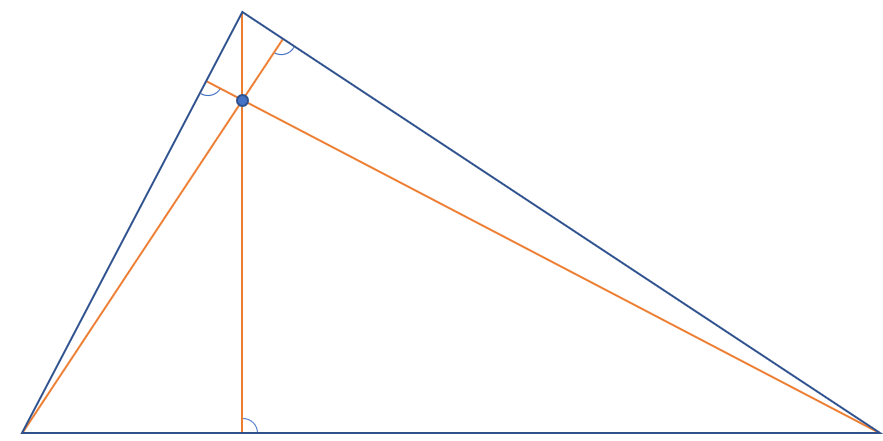
Az előbb felvett párhuzamos szakaszok tulajdonságai:
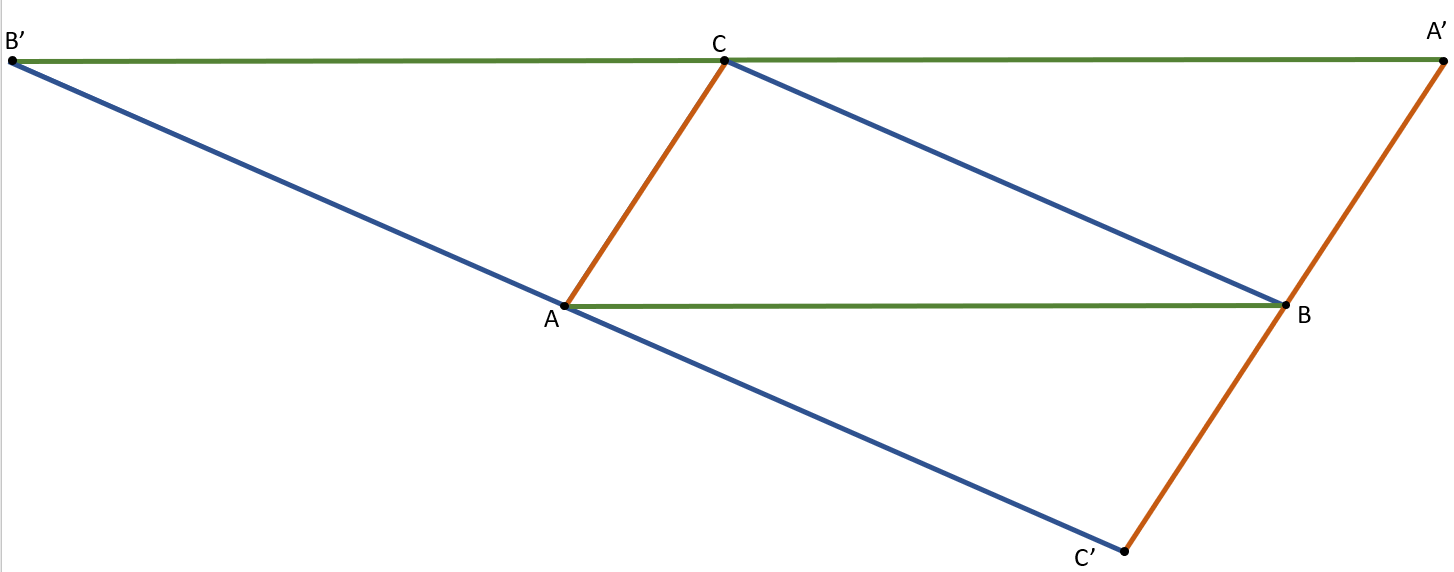
Mint láttuk, a belső háromszög egy egy oldala, megegyezik a külső háromszög vele párhuzamos oldalának a felével. Ebből következik, hogy pont fele olyan hosszú az adott belső oldal. Ezen tulajdonságok miatt az AB, BC és CA szakaszok középvonalai az A'B'C' háromszögnek.
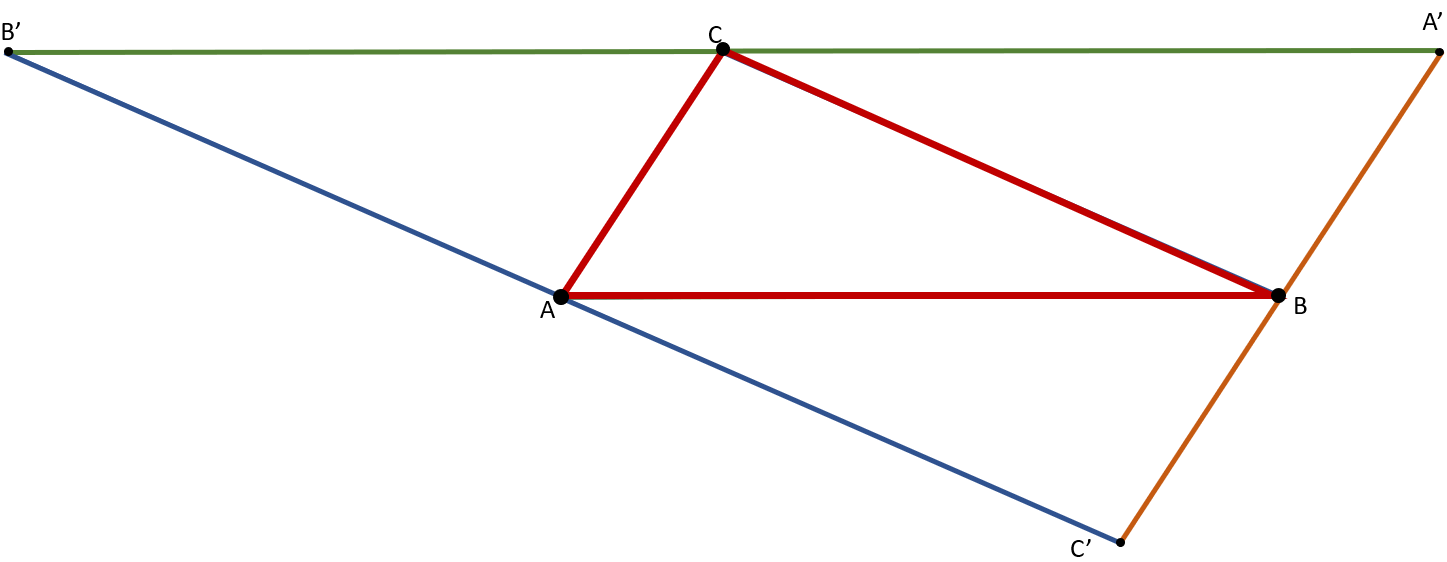
Ezután berajzoljuk az ABC háromszög magasságvonalait, amik az előbb bizonyítottak miatt oldalfelező merőlegesei az A'B'C' háromszögnek. Azt pedig tudjuk, hogy a háromszög magasságvonalai egy pontban metszik egymást.