Magasság tétel
Az általános magasságtétel az euklideszi geometria egyik elemi tétele, mely egy háromszög magasságát az oldalak (négyzetgyök-kifejezést tartalmazó) függvényében adja meg; kimondja, hogy egy háromszög három oldalának ismeretében kiszámítható a háromszög bármelyik magassága.
Bizonyítás
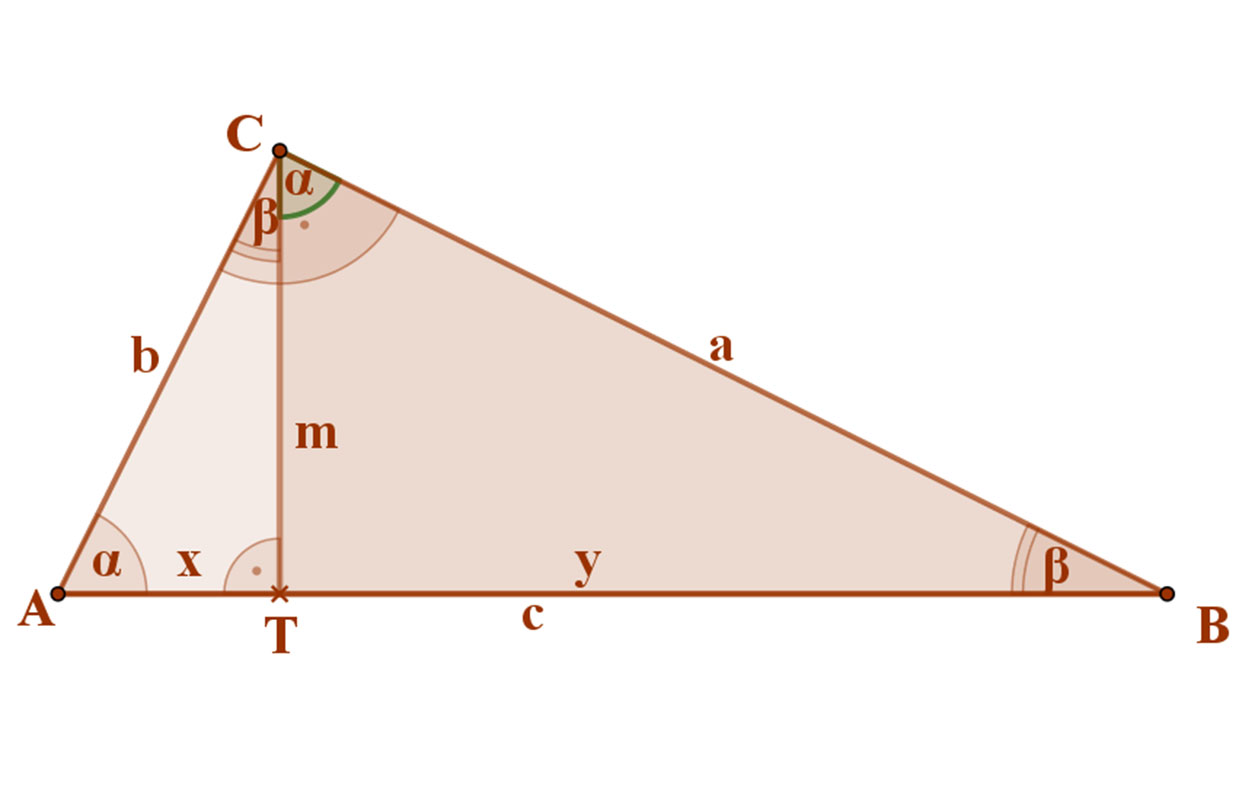
Az AB átfogóhoz tartozó magasság az ABC háromszöget két derékszögű háromszögre, az ATC és a BTC háromszögekre bontja.
Ezek háromszögek mindketten hasonlítanak az eredeti ABC háromszöghöz, mivel ezek is derékszögűek, és az egyik hegyes szögük közös. Az ATC háromszögben az α szög, míg a BTC háromszögben a ß szög közös. Emiatt persze a két kisebbik háromszög egymásra is hasonlít.
Tehát: ABCΔ ~ ATCΔ~ BTCΔ.
Mivel az ATCΔ~ BTCΔ , ezért a megfelelő oldalainak aránya egyenlő. Azaz
AT:TC=TC:TB, vagyis x:m=m:y.
Hiszen az m magasság az ATCΔ-ben az α szöggel, míg BTCΔ-ben a β szöggel van szemben.
A fenti aránypárt szorzat alakba írva: m2=x⋅y. Ez azt jelenti, hogy az átfogóhoz tartozó magasság mértani közepe az átfogó két szeletének.
Tehát az ábra szerint: m egyenlő x és y szorzatának gyökével.
Képlettel:
()
Megjegyzés
Az általános magasságtétel – amely tompaszögű háromszögekre ugyanúgy érvényes, mint a hegyesszögűekre és a derékszögűekre – bizonyítása a Pitagorasz-tételen alapulhat, és egyik fontos matematikai alkalmazását a Hérón-képlet levezetésében találjuk, mely utóbbi bizonyítása az általános magasságtételből tulajdonképp csak annyi, hogy egy új változót vezetünk be: a félkerületet.
Videó
videó letöltés
vissza az oldalra

