A súlyvonalak egy pontban metszik egymást
Bizonyítás:
A tétel: Az A, B, C csúcsból induló súlyvonalak (az a vonal, amely a háromszögben összeköt egy csúcsot a vele szemközti oldal felezőpontjával) egy pontban metszik egymást (súlypont)
Mivel FB és FC felezőpontok, ezért tudjuk, hogy ezt a két pontot összekötő szakasz párhuzamos a CB szakasszal.
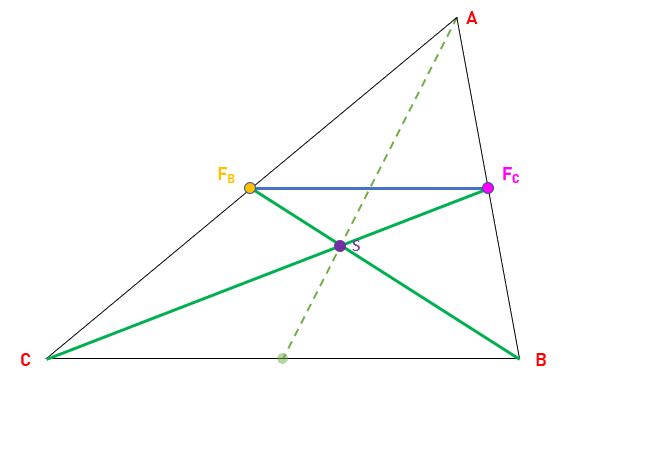
Ebből kiindulva tudjuk, hogy FBFCS háromszög hasonló a CBS háromszöggel. Mivel FB FC szakasz a két felezőpontból indul ki ez a háromszög középvonala, pontosabban a CB-hez tartozó középvonal, ezért tudjuk, hogy CB kétszer akkora és ebből, pedig az következik, hogy FBFCS háromszögnél is kétszer nagyobb a CBS.
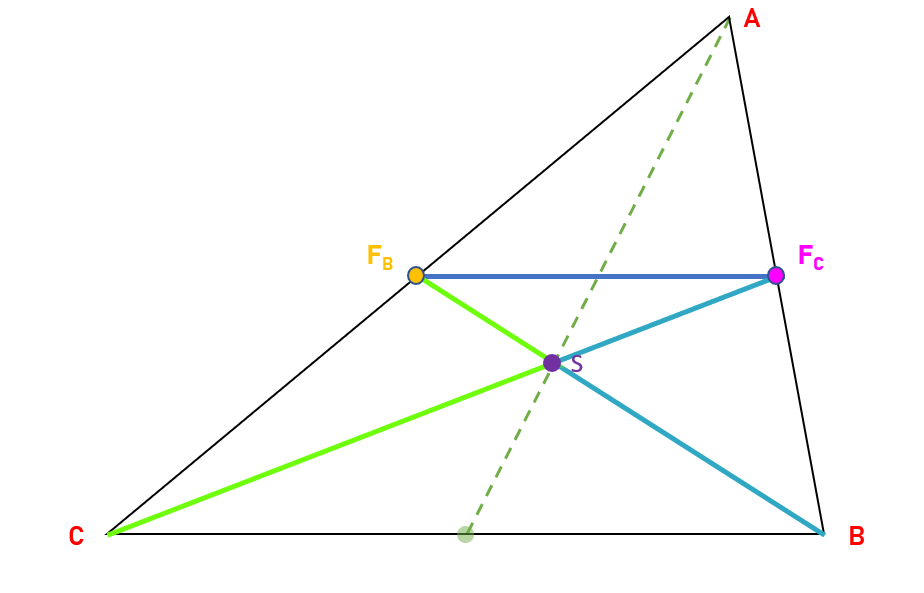
Mivel FCFBS háromszög fele akkora, mint CBS, ezért tudjuk, hogy az összes oldala is fele akkora tehát az S a BFB szakasz oldalhoz közelebbi harmadolópontja.
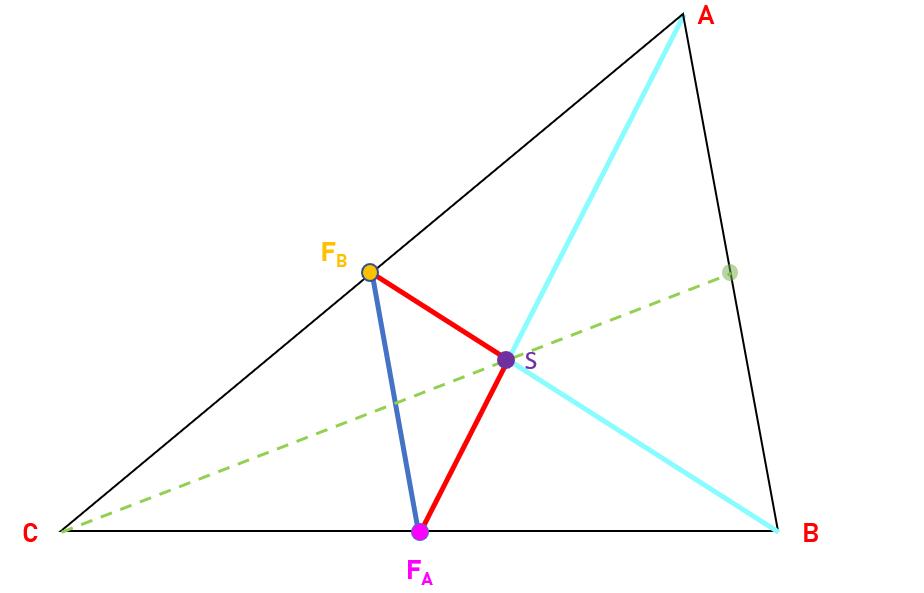
Ugyanennél a háromszögnél a CFC súlyvonal helyett az AFA súlyvonalat használjuk. Ebben az esetben, minden ugyanúgy igaz, mint CFC súlyvonalnál és, mivel mindkettő ugyanúgy az oldalhoz közelebbi harmadolópontnál metszik BFB súlyvonalat ezért tudjuk, hogy mindhárom ugyanott metszi egymást.