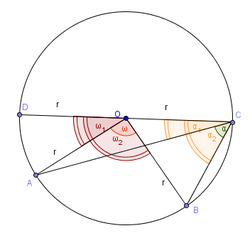
Kerületi és középponti szögek tétele
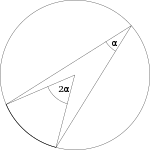
A kerületi és középponti szögek tétele kimondja, hogy adott körben adott ívhez tartozó középponti szög
(ω) mindig kétszerese az ívhez tartozó kerületi (α) szögnek.
2α = ω
A tétel bizonyításának letöltése
Bizonyítás
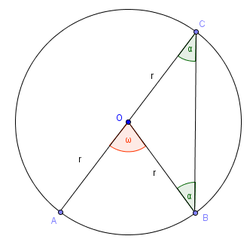
1. eset
A középponti szög egyik szára illeszkedik a kerületi szög egyik szárára. Legyen az adott kerületi szög a továbbiakban α, a középponti szög pedig ω. Az ábrán látható BCO háromszög egyenlő szárú, mert OC = OB = r, ezért C-nél és B-nél lévő szöge egyaránt α. Mivel ω ennek a háromszögnek külső szöge, egyenlő a két másik csúcsnál lévő belső szög összegével, azaz 2α = ω.
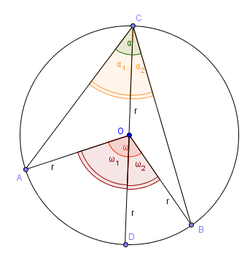
2. eset
A középponti szög a kerületi szög szögtartományába esik, nincs közös száruk. Vegyük fel a CO egyenest az ábra szerint, melynek a körrel való metszéspontja legyen D. A CD szakasz az α kerületi szöget α1 és α2 szögekre, ω középponti szöget ω1 és ω2 szögekre osztja. Az I. esetben beláttuk, hogy 2α1 = ω1 és 2α2 = ω2. Ezeket az egyenleteket összeadva kapjuk, hogy 2α1 + 2α2 = ω1 + ω2, vagyis 2α = ω.
3. eset
A középponti szög nem esik a kerületi szög szögtartományába. Vegyük fel a CO egyenest az ábra szerint, melynek a körrel való metszéspontja legyen D. Legyen DCA∠ = α1, DCB∠ = α2, DOA∠ = ω1, DOB∠ = ω2. Az I. esetben beláttuk, hogy 2α1 = ω1 és 2α2 = ω2. Az első egyenletből a másodikat kivonva kapjuk, hogy 2α2 - 2α1 = ω2 - ω1, vagyis 2α = ω.
