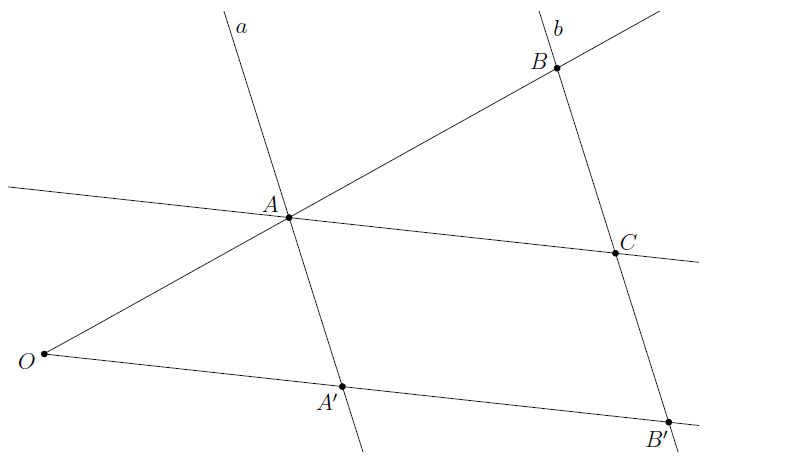
Van egy 𝑶 csúcsú szög, melynek szárait a párhuzamos a és b egyenesek metszik 𝑨 és 𝑨', illetve 𝑩 és 𝑩' pontokban.
Ekkor 𝑶𝑨/𝑶𝑩=𝑨𝑨′/𝑩𝑩′
Húzzunk párhuzamost Az 𝑨 ponton keresztül az 𝑶𝑩′-vel, ez a b egyenest 𝑪 pontban metszi. Az 𝑶𝑩𝑩′ szöget metszi az 𝑶𝑩′ és az 𝑨𝑪 egyenes.
Párhuzamos szelők tétele alapján: 𝑶𝑨:𝑶𝑩
A párhuzamos egyenespárok miatt 𝑨 𝑨' 𝑪 𝑩' paraleogramma
Paraleogramma miatt: 𝑪𝑩'=𝑨𝑨'
Ezt felhasználjuk az előző arányban => 𝑶𝑨:𝑶𝑩=𝑨𝑨':𝑩𝑩'