Ha egy körhöz egy külső “P” pontból szelőket húzunk, azt tapasztalhatjuk, hogy ahogy a szelő végigsöpör a körön, A “P” ponttól a távolabbi metszéspontokig terjedő szakaszok egy darabig növekednek, ugyanakkor a közelebbi metszéspontokig terjedő szakaszok csökkennek.
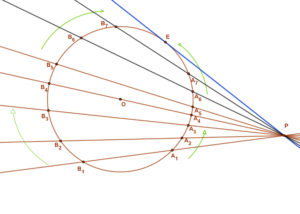
A “P” ponttól a távolabbi metszéspontokig terjedő szakaszok (PB1,PB2, PB3) egy darabig növekednek, ugyanakkor a közelebbi metszéspontokig terjedő szakaszok (PA1,PA2, PA3), csökkennek. Szélsőértéküket akkor érik el, amikor a szelő átmegy a kör középpontján. Ezután a folyamat megfordul és a két pont az “E” érintési pontban találkozik.
Ez azt mutatja, hogy ezek között a távolságok között (PBi, PAi, PE) kapcsolat van.
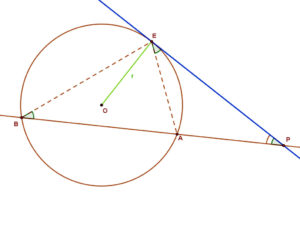
Húzzunk egy körhöz egy külső “P” pontból egy szelőt. Ennek a körrel való távolabbi metszéspontját jelöljük “B”-vel, a közelebbi metszéspontot pedig jelöljük “A”-val.

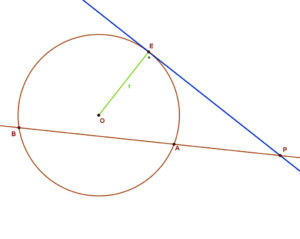
A körhöz egy külső pontból húzott érintőszakasz mértani közepe annak a két szakasznak, amelyek a külső pontra illeszkedő bármely szelőn a ponttól a körrel alkotott metszéspontokig terjednek. Vagyis: PE² = PB ∙ PA
Kössük össze a “B” és “A” metszéspontokat az “E” érintési ponttal. A PBE és PAE háromszögek hasonlóak, mert: az ABE szög egyenlő AEP szöggel, mert mindketten az AE ívhez tartozó kerületi szögek, másrészt a P csúcsnál lévő szögük közös. Ebből következik, hogy megfelelő oldalaiknak az aránya egyenlő.
Ebből .következik, hogy megfelelő oldalaiknak az aránya egyenlő. Azaz: PE:PB=PA:PE. Ezt szorzat alakba írva: PE² = PB ∙ PA